|
|
|
|
DOWNLOAD
Please click on the following link to download nano-archimedes:
http://www.nano-archimedes.com/download/nano-archimedes-ballistic-1D-2D-1body-2bodies-2.0.tar
This version of nano-archimedes implements the (ballistic) single- and two-body Wigner Monte Carlo method based on the signed particle
formulation of quantum mechanics.
This code is capable of simulating:
1) a one-dimensional Gaussian wave-packet going towards a potential barrier (video below),
2) a two-dimensional Gaussian wave-packet going towards a potential barrier (video below),
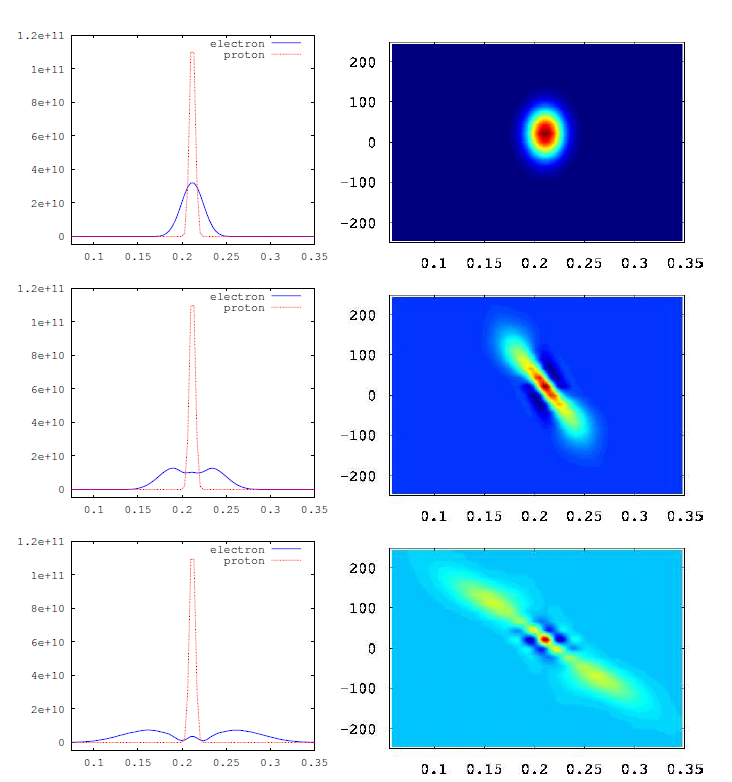
3) a one-dimensional two-body quantum system (picture below).
DOCUMENTATION
You can understand the algorithm developed in nano-archimedes and extend it to 2D and 3D spaces by reading this paper:
J.M. Sellier, M. Nedjalkov, I. Dimov, S. Selberherr,
A benchmark study of the Wigner Monte-Carlo method, Monte Carlo Methods and Applications,
De Gruyter, DOI: 10.1515/mcma-2013-0018, (2014).
You can utilize this code for density functional theory (DFT) calculations by following the details reported in the this paper:
J.M. Sellier, I. Dimov,
A Wigner Monte Carlo Approach to Density Functional Theory,
Journal of Computational Physics 270, pp. 265-277, (2014)
DOI: 10.1016/j.jcp.2014.03.065.
You can generalize this code to the time-dependent quantum many-body problem (ab-initio) by following the instructions reported in this
paper:
J.M. Sellier, I. Dimov,
The Many-body Wigner Monte Carlo Method for Time-dependent Ab-initio Quantum Simulations,
Journal of Computational Physics 273, pp. 589-597 (2014)
DOI: 10.1016/j.jcp.2014.05.039.
You can add phonon scattering to this code by reading the following paper:
J.M. Sellier, I. Dimov,
The Wigner-Boltzmann Monte Carlo method applied to electron transport in the presence of a single dopant,
Computer Physics Communications 185, pp. 2427-2435, (2014)
DOI: 10.1016/j.cpc.2014.05.013.
|
|
|
|
|
|
|
|
|
If you are interested in nano-archimedes, you have questions or suggestions, you want to know more about the code,
please, do not hesitate to contact us!

|
|
|
|
